

(This is the three-angle version.) Supplements of congruent angles are congruent. If two angles are each supplementary to a third angle, then they’re congruent to each other.
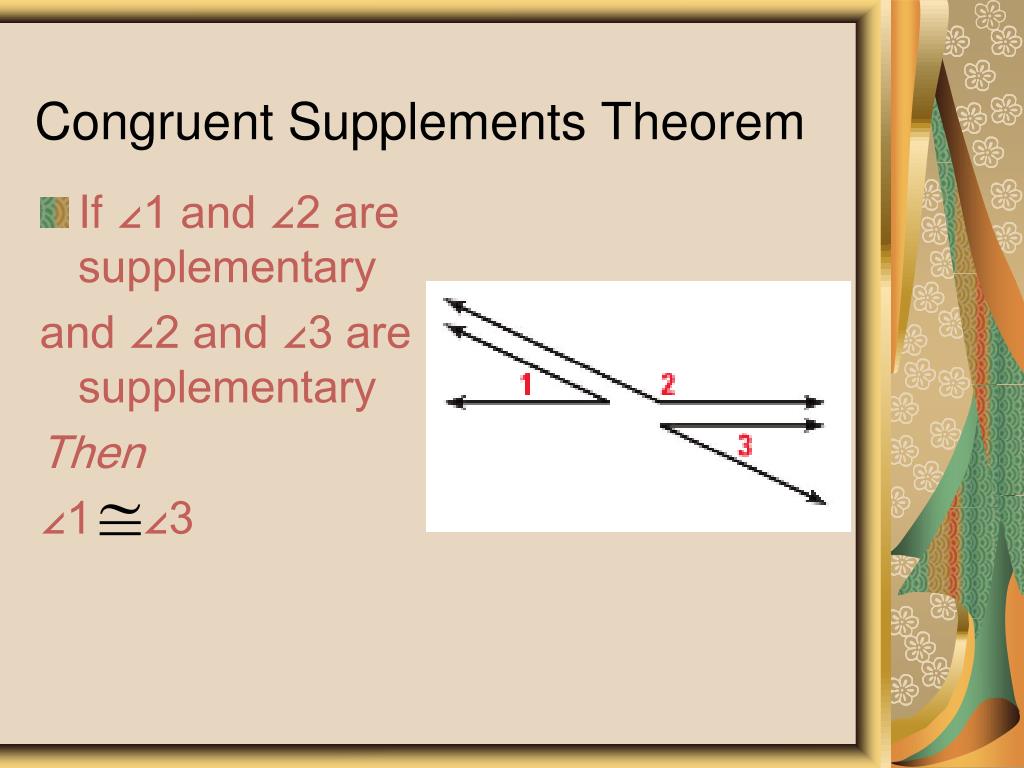
The rays corresponding to supplementary angles intersect the unit circles in points having the same $y$-coordinate, so the two angles have the same sine (and opposite cosines). Mathematical Practices 3 Construct viable arguments and critique the reasoning of others. And here are the two theorems about supplementary angles that work exactly the same way as the two complementary angle theorems: Supplements of the same angle are congruent. If you define the sine by means of the unit circle, then this image should explain the fact:

Let's stick to right triangles, which allow to define the sine for acute angles: if $\alpha=\widehat=\alpha'$, that is, $\alpha'=\pi-\alpha$, then Congruent supplementary angles are always both right angles in Euclidean geometry, and in this video we prove just that Supplementary angles are angles (oft. It depends a lot on how you define the sine.


 0 kommentar(er)
0 kommentar(er)
